Three (long) readings on data science
Put aside the turf battle
Data science and statistics have both overlap and difference. See Donoho Section 2.
Our concern is the extent to which we can make a statistics intro better by aiming it toward relevant parts of data science.
Six divisions of data science
(See Donohoe)
- Data Exploration and Preparation
- Data Representation and Transformation
- Computing with Data
- Data Modeling
- Data Visualization and Presentation
- Science about Data Science
- e.g. p-values are mis-used, false discovery
Group Activity: Look for overlap (and lack of overlap) between these six divisions and a hypothetical ideal statistics course. Use this document, copying it for your group.
Inference
- the Data Modeling culture
- the Algorithmic Modeling culture
Other aspects of dicotomy:
prediction vs inference (or estimation)
exploratory vs confirmatory analysis
forecasting vs intervention
Mixing together the two cultures leads to confusion and error
| Forecasting | Intervention |
|---|---|
| Significance is a tool for model building | Effect size is important |
| R2 quantifies success | Improve outcome (e.g. greater benefits, less cost) |
| Performance is what counts | Avoid unexpected consequences |
| Causation not important | Causation central |
| Covariates eat variance | Covariates for standardization/adjustment and to implement our models of causation |
Many of our Stat 101 techniques derive from the problem of forecasting … but we don’t actually engage forecasting itself much in the course.
- example: we do confidence intervals, but not so much prediction intervals
- the theoretical framework is about population vs sample.
- We want to make inferences about about the population, but don’t say why. What will we do with that information?
Population parameter vs sample statistic
Small n
Donoho points out that statistics is no stranger to big data. But a large amount of time and effort in intro stats focuses on issues relating to small data, e.g.
- z versus t
- significance – have we got anything at all?
Small n + no computing ☛ rules out cross validation as an inferential technique.
Consequence: we introduce “degrees of freedom” theory before any demonstration of the actual problem it addresses.
Significance good, no significance bad (fail to reject)
But accurately detecting lack of association does inform us:
- design data collection
- avoid overfitting
- confirm causal network hypotheses
Experiment … the gold standard
Pushing this perspective enables the traditionalist to use forecast technology to infer causation.
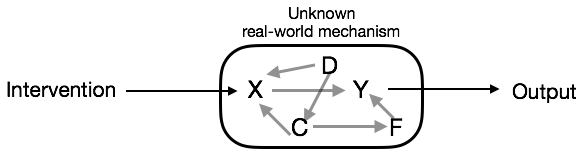
- If we can forecast outcome from exogenous intervention, we have demonstrated causation.
- It doesn’t matter what else is going on in the system! So we don’t have to worry about those other things.
But …
- it leaves out the many circumstances where decisions need to be made and no experiment has-yet-been/can-be done.
it provides no recourse for real/imperfect experiments.
historical analog: bimetalism